

(iv) The image of the point (-6, 5) in the y-axis is the point (-(-6), 5) i.e., (6, 5). (iii) The image of the point (0, 7) in the y-axis is the point (0, 7). (i) The image of the point (3, 4) in the y-axis is the point (-3, 4). Therefore, when a point is reflected in the y-axis, the sign of its abscissa changes.

Triangle DEF is formed by reflecting ABC across the x-axis and has vertices D (-6, -2), E (-4, -6) and F (-2, -4). x-axis reflectionĪ reflection across the x-axis changes the position of the y-coordinate of all the points in a figure such that (x, y) becomes (x, -y). Reflections in coordinate geometryīelow are three examples of reflections in coordinate plane.
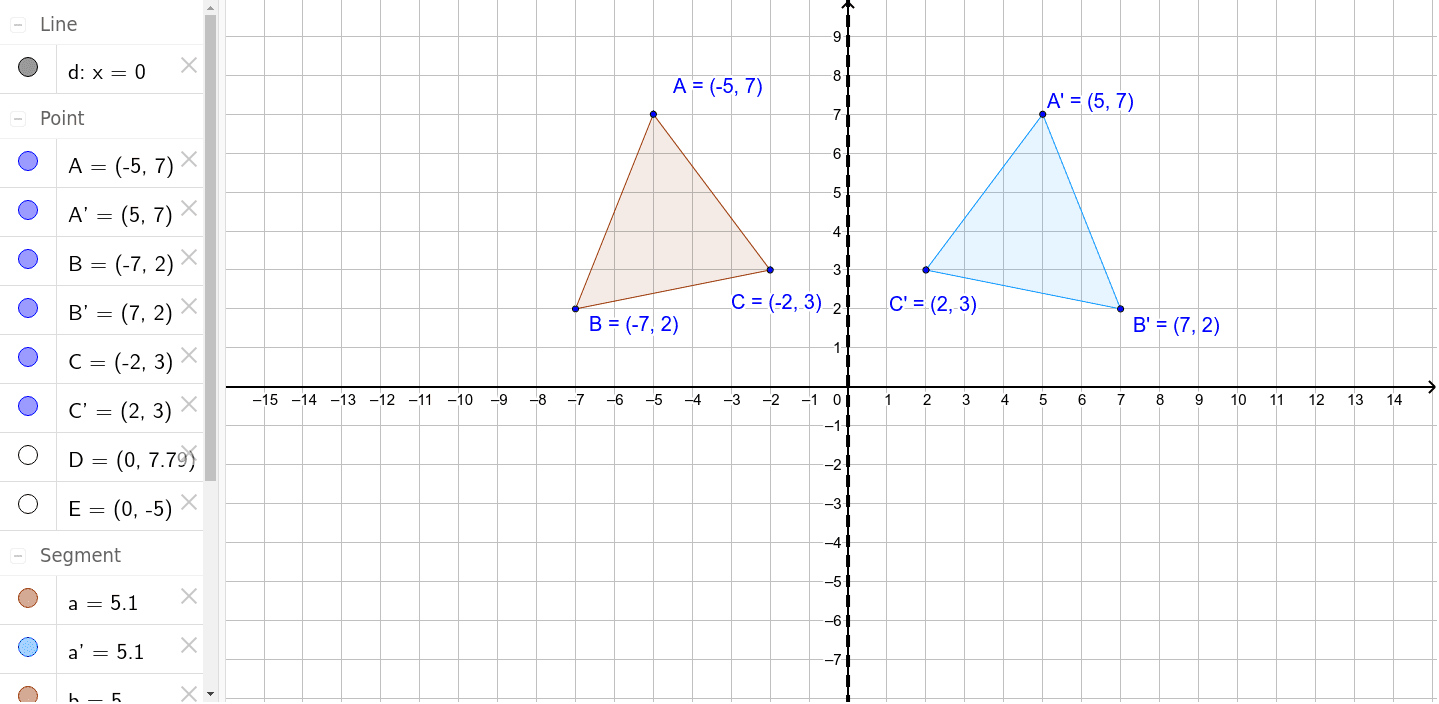
This is true for the distances between any corresponding points and the line of reflection, so line l is also a line of symmetry. Points A, B, and C on the pentagon are reflected across line l to A', B', and C'. Let line l be a line of reflection for the pentagon above. Whenever you reflect a figure across a line of reflection that is also a line of symmetry, each point on the figure is translated an equal distance across the line of symmetry, back on to the figure. You can think of folding half of the image of the butterfly across the line of reflection back on to its other half. The same result occurs if the left side of the butterfly is reflected across line l, so line l is also a line of symmetry. Reflecting the right side of the butterfly across line l maps it to the butterfly's left side. Reflection symmetryĪ line of reflection is also a line of symmetry if a geometric shape or figure can be reflected across the line back onto itself. This is true for any corresponding points on the two triangles. A, B, and C are the same distance from the line of reflection as their corresponding points, D, E, and F. In the figure above, triangle ABC is reflected across the line to form triangle DEF. For a 3D object, each point moves the same distance across a plane of refection. In a reflection of a 2D object, each point on the preimage moves the same distance across a line, called the line of reflection, to form a mirror image of itself. The term "preimage" is used to describe a geometric figure before it has been transformed and the term "image" is used to describe it after it has been transformed. A reflection is a rigid transformation, which means that the size and shape of the figure does not change the figures are congruent before and after the transformation. In geometry, a reflection is a type of transformation in which a shape or geometric figure is mirrored across a line or plane. Home / geometry / transformation / reflection Reflection


 0 kommentar(er)
0 kommentar(er)
